小優(yōu)智能科技有限公司成立于2015年底,是一家專注于高精度3D機(jī)器視覺模組研發(fā)、生產(chǎn)及銷售的高科技企業(yè)。
公司自主研發(fā)的3D機(jī)器視覺模組采用激光/DLP白光編碼光柵結(jié)構(gòu)光+雙工業(yè)相機(jī)方案,還原物體三維信息,廣泛應(yīng)用于消費(fèi)電子領(lǐng)域、工業(yè)領(lǐng)域和安防領(lǐng)域,具有精度高、速度快、成本低的優(yōu)勢(shì)。
基于局部特征描述子的點(diǎn)云配準(zhǔn)
傳統(tǒng)的點(diǎn)云配準(zhǔn)算法如icp算法在對(duì)兩組點(diǎn)云或多組點(diǎn)云進(jìn)行配準(zhǔn)時(shí),一般都需要點(diǎn)云具備比較好的初始對(duì)齊姿態(tài),這樣再使用迭代最近點(diǎn)的方法對(duì)兩兩點(diǎn)云進(jìn)行配準(zhǔn)。這種點(diǎn)云配準(zhǔn)方法在需要對(duì)齊點(diǎn)云的應(yīng)用場(chǎng)景中很常見。但他有比較強(qiáng)的限制條件,需要兩組點(diǎn)云有一個(gè)好的初始姿態(tài)。否則點(diǎn)云的配準(zhǔn)會(huì)陷入局部最優(yōu)解,無法完成點(diǎn)云間對(duì)齊。但在很多情況下,兩組點(diǎn)云沒有初始對(duì)齊姿態(tài),其初始姿態(tài)是完全未知的。這種情況,可以使用局部特征描述子對(duì)兩組點(diǎn)云進(jìn)行描述。局部特征描述子與點(diǎn)云姿態(tài)無關(guān),僅與點(diǎn)云及其臨近點(diǎn)云形成的局部特征有關(guān)。利用這種信息,可以有效的完成點(diǎn)云的初始配準(zhǔn),為后續(xù)基于迭代最近點(diǎn)的精細(xì)配準(zhǔn),提供良好的初始姿態(tài)。下面根據(jù)不同的特征描述,分別介紹特征直方圖(Point Feature Histograms,PFH)、快速點(diǎn)特征直方圖(Fast Point Feature Histograms, FPFH)、視點(diǎn)特征直方圖VFH(Viewpoint Feature Histogram)。并分析他們的區(qū)別及優(yōu)缺點(diǎn)。
引言
一堆離散的樣點(diǎn),只包含相對(duì)于某個(gè)坐標(biāo)系下的位置參數(shù),雖然能在空間中比較好的顯示出物體的樣子來,但對(duì)于視覺來說,這是遠(yuǎn)遠(yuǎn)不夠的。之所以在文章的題目中提到特征,就是希望能用特征的方法,達(dá)到視覺識(shí)別的功能。
離散點(diǎn)云,除了坐標(biāo)信息外,最為直觀的特征就是點(diǎn)、法向、曲率,這是最簡(jiǎn)單的特征,也是最忠實(shí)于原始點(diǎn)云的,這些特征包含了點(diǎn)云的最為詳細(xì)的數(shù)據(jù),雖然很少直接的使用,但在這個(gè)特征的基礎(chǔ)上,可以實(shí)現(xiàn)更高層次的識(shí)別。計(jì)算簡(jiǎn)單,速度快是這些基礎(chǔ)特征的特點(diǎn)之一,但是在進(jìn)行物體識(shí)別的時(shí)候,在大場(chǎng)景中,擁有相似法向或曲率的區(qū)域太多了,這就從一定程度上削弱了它的作用。
1. PFH
1.1 PFH原理
正如點(diǎn)特征表示法所示,表面法線和曲率估計(jì)是某個(gè)點(diǎn)周圍的幾何特征基本表示法。雖然計(jì)算非常快速容易,但是無法獲得太多信息,因?yàn)樗鼈冎皇褂煤苌俚膸讉€(gè)參數(shù)值來近似表示一個(gè)點(diǎn)的k鄰域的幾何特征。然而大部分場(chǎng)景中包含許多特征點(diǎn),這些特征點(diǎn)有相同的或者非常相近的特征值,因此采用點(diǎn)特征表示法,其直接結(jié)果就減少了全局的特征信息。本小節(jié)介紹三維特征描述子中的一位成員:點(diǎn)特征直方圖(Point Feature Histograms),我們簡(jiǎn)稱為PFH,本小節(jié)將介紹它的理論優(yōu)勢(shì),從PCL實(shí)現(xiàn)的角度討論其實(shí)施細(xì)節(jié)。PFH特征不僅與坐標(biāo)軸三維數(shù)據(jù)有關(guān),同時(shí)還與表面法線有關(guān)。
PFH計(jì)算方式通過參數(shù)化查詢點(diǎn)與鄰域點(diǎn)之間的空間差異,并形成一個(gè)多維直方圖對(duì)點(diǎn)的k鄰域幾何屬性進(jìn)行描述。直方圖所在的高維超空間為特征表示提供了一個(gè)可度量的信息空間,對(duì)點(diǎn)云對(duì)應(yīng)曲面的6維姿態(tài)來說它具有不變性,并且在不同的采樣密度或鄰域的噪音等級(jí)下具有魯棒性。點(diǎn)特征直方圖(PFH)表示法是基于點(diǎn)與其k鄰域之間的關(guān)系以及它們的估計(jì)法線,簡(jiǎn)言之,它考慮估計(jì)法線方向之間所有的相互作用,試圖捕獲最好的樣本表面變化情況,以描述樣本的幾何特征。因此,合成特征超空間取決于每個(gè)點(diǎn)的表面法線估計(jì)的質(zhì)量。如圖1所示,表示的是一個(gè)查詢點(diǎn)(Pq) 的PFH計(jì)算的影響區(qū)域,Pq 用紅色標(biāo)注并放在圓球的中間位置,半徑為r, (Pq)的所有k鄰元素(即與點(diǎn)Pq的距離小于半徑r的所有點(diǎn))全部互相連接在一個(gè)網(wǎng)絡(luò)中。最終的PFH描述子通過計(jì)算鄰域內(nèi)所有兩點(diǎn)之間關(guān)系而得到的直方圖,因此存在一個(gè)O(k) 的計(jì)算復(fù)雜性。
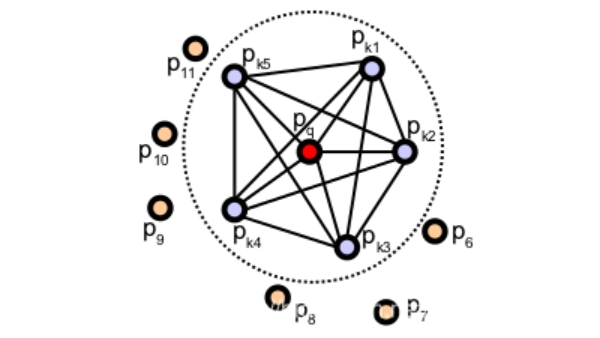
圖1 查詢點(diǎn) 的PFH計(jì)算的影響區(qū)域
為了計(jì)算兩點(diǎn)Pi和Pj及與它們對(duì)應(yīng)的法線Ni和Nj之間的相對(duì)偏差,在其中的一個(gè)點(diǎn)上定義一個(gè)固定的局部坐標(biāo)系,如圖2所示。
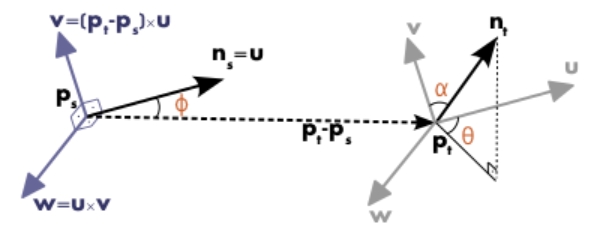
圖2 定義一個(gè)固定的局部坐標(biāo)系
為查詢點(diǎn)創(chuàng)建最終的PFH表示,所有的四元組將會(huì)以某種統(tǒng)計(jì)的方式放進(jìn)直方圖中,這個(gè)過程首先把每個(gè)特征值范圍劃分為b個(gè)子區(qū)間,并統(tǒng)計(jì)落在每個(gè)子區(qū)間的點(diǎn)數(shù)目,因?yàn)樗姆种奶卣髟谏鲜鲋袨榉ň€之間的角度計(jì)量,在三角化圓上可以將它們的參數(shù)值非常容易地歸一到相同的區(qū)間內(nèi)。一個(gè)統(tǒng)計(jì)的例子是:把每個(gè)特征區(qū)間劃分成等分的相同數(shù)目,為此在一個(gè)完全關(guān)聯(lián)的空間內(nèi)創(chuàng)建有b個(gè)區(qū)間的直方圖。在這個(gè)空間中,一個(gè)直方圖中某一區(qū)間統(tǒng)計(jì)個(gè)數(shù)的增一對(duì)應(yīng)一個(gè)點(diǎn)的四個(gè)特征值。
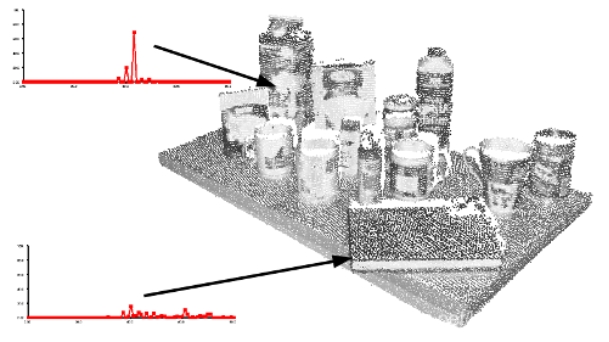
圖3 點(diǎn)云中不同點(diǎn)的點(diǎn)特征直方圖表示法
1.3 PFH的總結(jié)
點(diǎn)特征的描述子一般是基于點(diǎn)坐標(biāo)、法向量、曲率來描述某個(gè)點(diǎn)周圍的幾何特征。用點(diǎn)特征描述子不能提供特征之間的關(guān)系,減少了全局特征信息。因此誕生了一直基于直方圖的特征描述子:PFH–point feature histogram(點(diǎn)特征直方圖)。
PFH通過參數(shù)化查詢點(diǎn)和緊鄰點(diǎn)之間的空間差異,形成了一個(gè)多維直方圖對(duì)點(diǎn)的近鄰進(jìn)行幾何描述,直方圖提供的信息對(duì)于點(diǎn)云具有平移旋轉(zhuǎn)不變性,對(duì)采樣密度和噪聲點(diǎn)具有穩(wěn)健性。PFH是基于點(diǎn)與其鄰近之間的關(guān)系以及它們的估計(jì)法線,也即是它考慮估計(jì)法線之間的相互關(guān)系,來描述幾何特征。
PFH的缺點(diǎn):
計(jì)算復(fù)雜度高。已知點(diǎn)云P中有n個(gè)點(diǎn),假設(shè)點(diǎn)云均勻密度,每點(diǎn)在鄰域半徑r內(nèi)平均可以選到k個(gè)近鄰,該算法對(duì)每個(gè)點(diǎn)來說計(jì)算PFH的時(shí)間復(fù)雜度為O(k^2),那么它的點(diǎn)特征直方圖(PFH)的理論計(jì)算復(fù)雜度就是 O(nk2)。對(duì)于實(shí)時(shí)應(yīng)用或接近實(shí)時(shí)應(yīng)用中,密集點(diǎn)云的點(diǎn)特征直方圖(PFH)的計(jì)算,O(nk2)的計(jì)算復(fù)雜度實(shí)在不敢恭維,是一個(gè)主要的性能瓶頸。
2. FPFH
2.1 FPFH原理
快速點(diǎn)特征直方圖(Fast Point Feature Histograms, FPFH)是PFH計(jì)算方式的簡(jiǎn)化形式。它的思想在于分別計(jì)算查詢點(diǎn)的k鄰域中每一個(gè)點(diǎn)的簡(jiǎn)化點(diǎn)特征直方圖(Simplified Point Feature Histogram,SPFH),再通過一個(gè)公式將所有的SPFH加權(quán)成最后的快速點(diǎn)特征直方圖。FPFH把算法的計(jì)算復(fù)雜度降低到了O(nk) ,但是任然保留了PFH大部分的識(shí)別特性。
FPFH計(jì)算過程:
只計(jì)算每個(gè)查詢點(diǎn)Pq和它鄰域點(diǎn)之間的三個(gè)特征元素(參考PFH),在這里不同于PFH:PFH是計(jì)算鄰域點(diǎn)所有組合的特征元素,而這一步只計(jì)算查詢點(diǎn)和近鄰點(diǎn)之間的特征元素。如下圖,第一個(gè)圖是PFH計(jì)算特征過程,即鄰域點(diǎn)所有組合的特征值(圖中所有連線,包括但不限于Pq和Pk之間的連線),第二個(gè)圖是FPFH的計(jì)算內(nèi)容,只需要計(jì)算Pq(查詢點(diǎn))和緊鄰點(diǎn)(圖2中紅線部分)之間的特征元素。可以看出降低了復(fù)雜度我們稱之為SPFH(simple point feature histograms)。
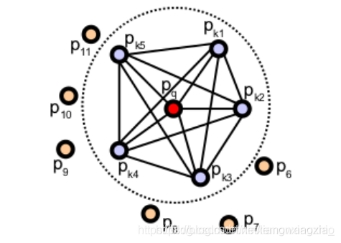
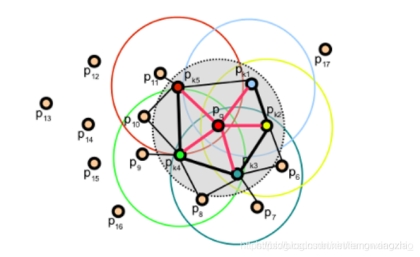
2.2 FPFH與PFH的主要區(qū)別
FPFH沒有對(duì)全互連點(diǎn)的所有鄰近點(diǎn)的計(jì)算參數(shù)進(jìn)行統(tǒng)計(jì),因此可能漏掉了一些重要的點(diǎn)對(duì),而這些漏掉的對(duì)點(diǎn)可能對(duì)捕獲查詢點(diǎn)周圍的幾何特征有貢獻(xiàn)。PFH特征模型是對(duì)查詢點(diǎn)周圍的一個(gè)精確的鄰域半徑內(nèi),而FPFH還包括半徑r范圍以外的額外點(diǎn)對(duì)(但不超過2r的范圍);因?yàn)椴捎脵?quán)重計(jì)算的方式,所以FPFH結(jié)合SPFH值,重新捕獲鄰近重要點(diǎn)對(duì)的幾何信息;由于大大地降低了FPFH的整體復(fù)雜性,因此FPFH有可能使用在實(shí)時(shí)應(yīng)用中。
3. VFH
3.1 VFH原理
視點(diǎn)特征直方圖VFH(Viewpoint Feature Histogram)描述子,它是一種新的特征表示形式,應(yīng)用在點(diǎn)云聚類識(shí)別和六自由度位姿估計(jì)問題。下圖展示了VFH識(shí)別和位姿估計(jì)的一個(gè)例子。已知一組訓(xùn)練樣本數(shù)據(jù)(除最左端的點(diǎn)云之外的首行,底行),學(xué)習(xí)了一個(gè)模型,然后使用一個(gè)點(diǎn)云(左下方)來查詢/測(cè)試這個(gè)模型。從左下方開始,匹配結(jié)果從左到右是按照最好到最壞的順序排列的。
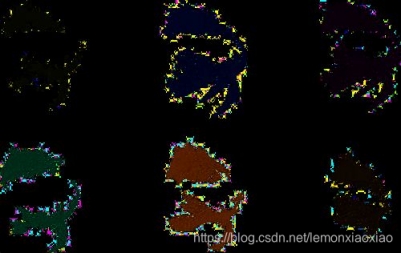
視點(diǎn)特征直方圖(或VFH)是源于FPFH描述子(見Fast Point Feature Histograms (PFH) 描述子)。由于它的獲取速度和識(shí)別力,我們決定利用FPFH強(qiáng)大的識(shí)別力,但是為了使構(gòu)造的特征保持縮放不變性的性質(zhì)同時(shí),還要區(qū)分不同的位姿,計(jì)算時(shí)需要考慮加入視點(diǎn)變量。我們做了以下兩種計(jì)算來構(gòu)造特征,以應(yīng)用于目標(biāo)識(shí)別問題和位姿估計(jì):
擴(kuò)展FPFH,使其利用整個(gè)點(diǎn)云對(duì)象來進(jìn)行計(jì)算估計(jì)(如下圖所示),在計(jì)算FPFH時(shí)以物體中心點(diǎn)與物體表面其他所有點(diǎn)之間的點(diǎn)對(duì)作為計(jì)算單元。2. 添加視點(diǎn)方向與每個(gè)點(diǎn)估計(jì)法線之間額外的統(tǒng)計(jì)信息,為了達(dá)到這個(gè)目的,我們的關(guān)鍵想法是在FPFH計(jì)算中將視點(diǎn)方向變量直接融入到相對(duì)法線角計(jì)算當(dāng)中。
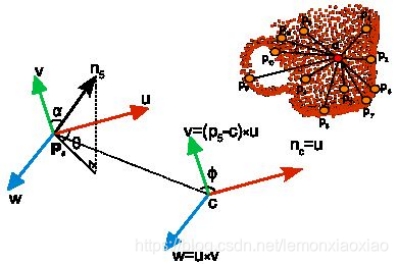
通過統(tǒng)計(jì)視點(diǎn)方向與每個(gè)法線之間角度的直方圖來計(jì)算視點(diǎn)相關(guān)的特征分量。注意:并不是每條法線的視角,因?yàn)榉ň€的視角在尺度變換下具有可變性,我們指的是平移視點(diǎn)到查詢點(diǎn)后的視點(diǎn)方向和每條法線間的角度。第二組特征分量就是前面PFH中講述的三個(gè)角度,如PFH小節(jié)所述,只是現(xiàn)在測(cè)量的是在中心點(diǎn)的視點(diǎn)方向和每條表面法線之間的角度,如下圖所示。

因此新組合的特征被稱為視點(diǎn)特征直方圖(VFH)。下圖表體現(xiàn)的就是新特征的想法,包含了以下兩部分:
1. 一個(gè)視點(diǎn)方向相關(guān)的分量
2. 一個(gè)包含擴(kuò)展FPFH的描述表面形狀的分量
如有侵權(quán),聯(lián)系刪除